
对递归类算法的小总结
writer:lIcht email:lIcht.gzl@gmail.com date: 2019.10.1
最近刷leetcode时遇到的树类题目的解答多半是对迭代方法的训练,想不到窍门可能那一小时就白白没了。递归、迭代类题目做得好不好的区别可能就是几十行代码和两三行代码的区别了,惊叹评论区大佬简单几行代码的神级操作,有时连光看都要理解半天,也多亏这些大佬的解答,也给我带来了很多技巧上的帮助,对递归类的题目也不会像以前那样无从下手了,这类题目同样存在某些套路。
递归三部曲
面对一道递归类的题目,我们总会忍不住想着从最开始怎么一层一层迭代,把每层的迭代细节都想明白,以至于越想越多越想越复杂,陷入困境。其实在着手递归问题应该从大局入手,首先要思考的是在一次迭代中的问题,也只需要重点考虑仅仅一次递归的流程就好了,比如这次递归中的出口、操作、返回值等。总的来说可以分为三步:
1、找整个递归的终止条件:递归应该在什么时候结束?
2、找返回值:应该给上一级返回什么信息?
3、本级递归应该做什么:在这一级递归中,应该完成什么任务?
接下来是leetcode里面的例子:
例子
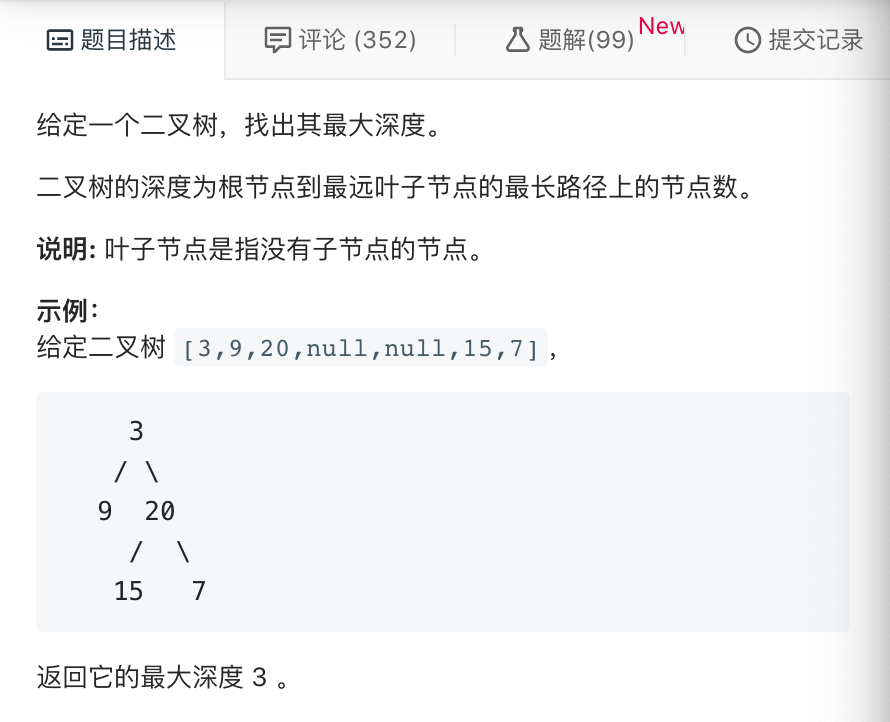
一、寻找二叉树的最大深度:
解题过程:
1、递归的终止条件:当然是树为空的时候,此时树的深度为0,递归就结束了。
2、递归的返回值:最大深度,也就是一次递归中两子树之中的最大深度,整形数值。
3、先思考在此次递归中,一次递归要处理哪些东西,无疑是一个节点以及其两个子节点,需要得到他们的高度信息,返回两个子节点的深度的最大值。那么本级递归应该做什么就很明确了,自然就是在root的左右子树中选择较大的一个,再加上1就是以root为根的子树的最大深度了,然后再返回这个深度即可。
Python实现方式如下:
class Solution(object): def maxDepth(self, root): """ :type root: TreeNode :rtype: int """ if not root: return 0 return max(self.maxDepth(root.left), self.maxDepth(root.right))+1 Java实现方式:
xxxxxxxxxxclass Solution { public int maxDepth(TreeNode root) { //终止条件:当树为空时结束递归,并返回当前深度0 if(root == null){ return 0; } //root的左、右子树的最大深度 int leftDepth = maxDepth(root.left); int rightDepth = maxDepth(root.right); //返回的是左右子树的最大深度+1 return Math.max(leftDepth, rightDepth) + 1; }}
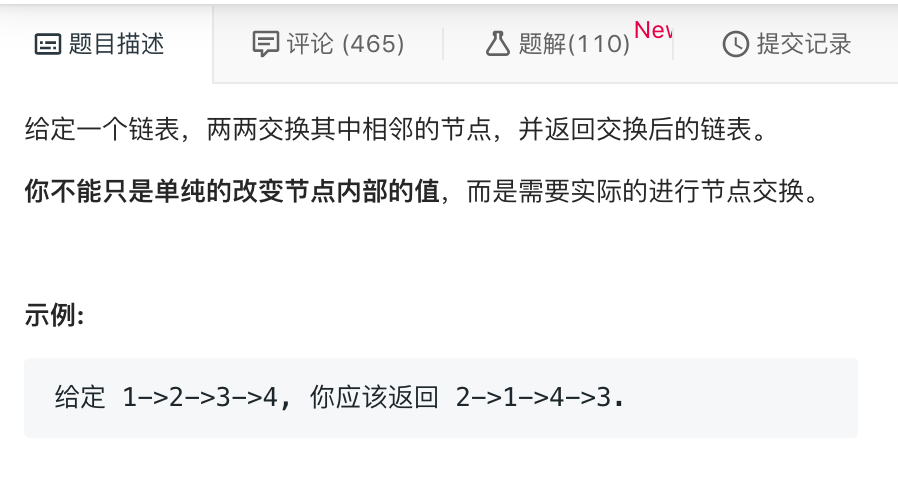
二、两两交换链表中的节点:
解题过程:
1、递归终止条件:剩下一个或者当前为最后节点时,就没办法进行一次交换了,此时返回。此时返回链表头。
2、递归的返回值:返回已处理结束的链表头,也就是已经交换结束后的链表头。
3、一次递归的处理:要交换链表的前两个节点,然后将已处理的链表(function(list_rest))拼接到这两个节点后。node 记录的head.next的位置会跟着 head.next 与 head的交换一起动,之中指向head.next这一地址,所以返回上一级的链表的头始终是head.next也就是nede.next(在一次过程中会head与head.next的位置,所以node会被换到最前面)
Python实现方式:
xxxxxxxxxxclass Solution(object): def swapPairs(self, head): """ :type head: ListNode :rtype: ListNode """ if head is None or head.next is None: return head node = ListNode(None) node = head.next head.next = self.swapPairs(node.next) node.next = head return node Java实现方式:
xxxxxxxxxxclass Solution { public ListNode swapPairs(ListNode head) { //终止条件:链表只剩一个节点或者没节点了,没得交换了。返回的是已经处理好的链表 if(head == null || head.next == null){ return head; } //一共三个节点:head, next, swapPairs(next.next) //下面的任务便是交换这3个节点中的前两个节点 ListNode next = head.next; head.next = swapPairs(next.next); next.next = head; //根据第二步:返回给上一级的是当前已经完成交换后,即处理好了的链表部分 return next; }}
三、判断平衡二叉树:

解题过程:
1、递归的终止条件:子树为空的时候,空树自然是平衡二叉树了。
2、递归的返回信息:由题意不难知道应该返回bool类型,但是在递归中要传递返回处理的应该是节点的信息才对,最后才对平衡与否进行判断返回bool类型,因此,我们可以新定义一个函数来记录节点深度信息并判断节点是否是平衡二叉树。
3、目前树有三个节点:root,left,right。我们首先判断left子树和right子树是否是平衡二叉树,如果不是则直接返回false。再判断两树高度差是否不大于1,如果大于1也直接返回false。否则说明以root为节点的子树是平衡二叉树,那么就返回true和它的高度。
Python实现方式:
xxxxxxxxxxclass Solution(object): def isBalanced(self, root): """ :type root: TreeNode :rtype: bool """ if not root: return True elif abs(self.depth(root.left)-self.depth(root.right)) > 1: return False return self.isBalanced(root.left) and self.isBalanced(root.right) def depth(self, node): if not node: return 0 return max(self.depth(node.left), self.depth(node.right))+1Java实现方式:
xxxxxxxxxxclass Solution { //这个ReturnNode是参考我描述的递归套路的第二步:思考返回值是什么 //一棵树是BST等价于它的左、右俩子树都是BST且俩子树高度差不超过1 //因此我认为返回值应该包含当前树是否是BST和当前树的高度这两个信息 private class ReturnNode{ boolean isB; int depth; public ReturnNode(int depth, boolean isB){ this.isB = isB; this.depth = depth; } } //主函数 public boolean isBalanced(TreeNode root) { return isBST(root).isB; } //参考递归套路的第三部:描述单次执行过程是什么样的 //这里的单次执行过程具体如下: //是否终止->没终止的话,判断是否满足不平衡的三个条件->返回值 public ReturnNode isBST(TreeNode root){ if(root == null){ return new ReturnNode(0, true); } //不平衡的情况有3种:左树不平衡、右树不平衡、左树和右树差的绝对值大于1 ReturnNode left = isBST(root.left); ReturnNode right = isBST(root.right); if(left.isB == false || right.isB == false){ return new ReturnNode(0, false); } if(Math.abs(left.depth - right.depth) > 1){ return new ReturnNode(0, false); } //不满足上面3种情况,说明平衡了,树的深度为左右俩子树最大深度+1 return new ReturnNode(Math.max(left.depth, right.depth) + 1, true); }}更多相关题型 :
参考原文出处:http://39.96.217.32/blog/4